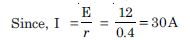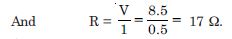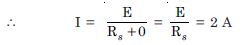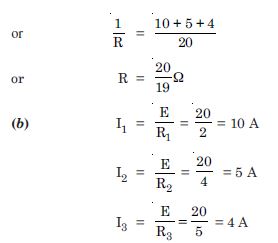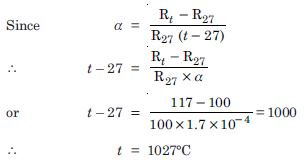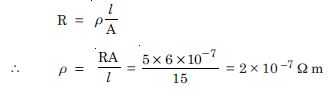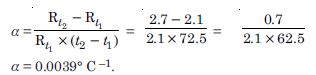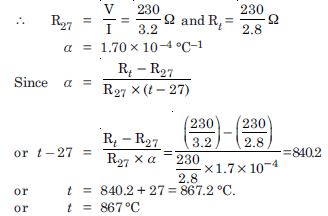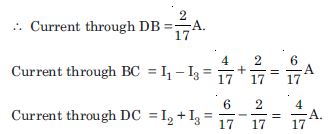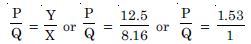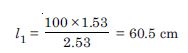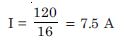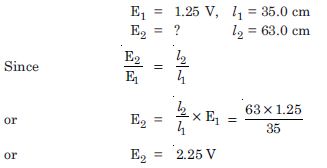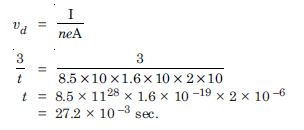Aasoka consists of top-quality educational resources including NCERT Solutions for Class 12th. These solutions are available for free for students and come in handy at the time of revision. Students can efficiently boost their skills with the help of NCERT Solutions. The questions are designed keeping the latest syllabus in mind. This aids students of Class 12th to achieve the desired marks in their board examinations.
In chapter 3 of Physics Class 12th “Current Electricity”, students will learn cell EMF, resistivity, internal resistance, conductance, drift velocity, graphing of internal resistance and resistivity, conversion of complex circuits into simple series, potentiometer, and various problems based on the concepts related to the chapter.
Question 1:
A storage battery of a car has an e.m.f. of 12V. If the internal resistance of the battery is 0.4 , what is the maximum current that can be drawn from the battery ?
Answer:
Given
E = 12V, r = 0.4 , I = ?
Question 2:
A battery of e.m.f. 10V and internal resistance 3 is connected to a resistor. If the current in the circuit is 0.5A, what is the resistance of the resistor ? What is the terminal voltage of the battery when the circuit is closed ?
Answer:
Given
E = 10V, r = 3, I = 0.5, R = ?
Since V = E – Ir
or V = 10 – 0.5 × 3
or V = 8·5 volt
Question 3:
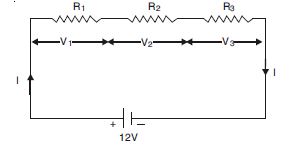
Three resistors 1 , 2 and 3 are combined in series. What is the total resistance of the combination ?
If the combination is connected to a battery of e.m.f. 12 V and negligible internal resistance, obtain the potential drop across each resistor.
Answer:
Given
R1 = 1 , R2 = 2 , R3. = 3
(a) Total resistance of series combination
Rs = R 1 + R2 + R3.
or Rs = 1 + 2 + 3 = 6
(b) Since E = I(R + r)
∴ V1. = IR1 = 2 × 1 = 2 V
V2. = IR2 = 2 × 2 = 4 V
V3. = IR3 = 2 × 3 = 6 V
Question 4:
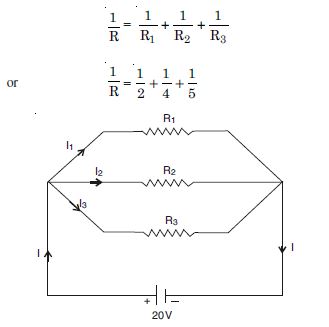
Three resistors 2 , 4 and 5 are combined in parallel. What is the total resistance of the combination ?
If the combination is connected to a battery of e.m.f. 20 V and negligible internal resistance, determine the current through each resistor, and the total current drawn from the battery.
Answer:
Given R 1 = 2 , R 2 = 4 , R 3 = 5
(a) Total resistance in parallel combination
Question 5:
At room temperature (27.0C) the resistance of a heating element is 100 . What is the temperature of the element if the resistance is found to be 117 , given that the temperature coefficient of the material of the resistor is 1.70 × 10 –4 C –1 ?
Answer:
Given
R 27 =100 , Rt = 117 , α = 1.70 × 10 –4 C –1, t = ?
Question 6:
A negligibly small current is passed through a wire of length 15 m and uniform crosssection 6.0 × 10 –7 m2 and its resistance is measured to be 5.0 . What is the resistivity of the material at the temperature of the experiment ?
Answer:
l =15 m, A = 6.0 × 10 –7 m2., R = 5.0
Applying the relation,
Question 7:
A silver wire has a resistance of 2.1 at 27.5 C, and a resistance of 2.7 at 100 C. Determine the temperature co-efficient of resistivity of silver.
Answer:
Rt1 =R27.5 = 2.1 and R t2 = R100 = 2.7
Question 8:
A heating element using nichrome connected to a 230 V supply draws an initial current of 3.2 A which settles after a few seconds to a steady value of 2.8 A. What is the steady temperature of the heating element if the room temperature is 27.0 C ? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is 1.70 × 10 –4 C –1.
Answer:
Given
V = 230 V, I = 2.8 A
Question 9:
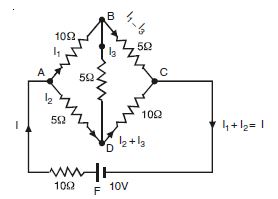
Determine the current in each branch of the following network :
Answer:
Applying Kirchhoff’s 2nd law of closed circuits ABD and BCD,
10I1 + 5I3 – 5I2 = 0
or 2I1 + I3 – I2 = 0 ....(1)
5 (I 1 – I 3) – 10 (I 2 + I 3) – 5I 3
= 0
5I1 – 10I2 – 20I3 = 0
or I1 – 2I2 – 4I3 = 0 ...(2)
Multiply (1) by 4 and add (2),
I1 – 2I2 – 4I3 = 0
8I1 – 4I2 + 4I3 = 0
9I1 – 6I2 = 0
3I1 – 2I2 = 0 ....(3)
Again applying Kirchhoffs law to closed ckt ADCBA
10I + 5I2 + 10 (I2 + I3) = 10
10 (I1 + I2) + 5I2 + 10 (I2 + I3)= 10
10I1 + 25I2 + 10I3 = 10
2I1 + 5I2 + 2I3 = 2 ...(4)
Multiplying (1) by 2 and subtracting from (4),
4I1 – 2I2 + 2I3 = 0
2I1 + 5I2 + 2I3 = 2
(4)
2I1 – 7I2 + 0 = – 2
or 6I1 – 21I2 = – 6 ...(5)
Multiplying (3) by 2 and subtracting from (5),
6I1 – 4I2 = 0
6I1 – 21I2 = – 6
– + –
Question 10:
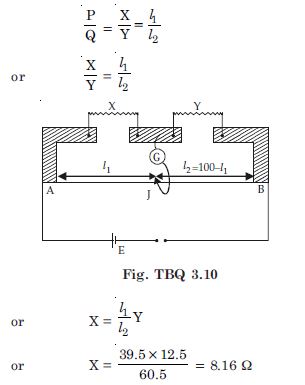
In a meter bridge the balance point is found to be at 39.5 cm from the end A, when the resistor Y is of 12.5 . Determine the resistance of X. Why are the connections between resistors in a Wheatstone or meter bridge made of thick copper strips ?
Determine the balance point of the meter bridge if X and Y are interchanged. What happens if the galvanometer and cell are interchanged at the balance point of the bridge ? Would the galvanometer show any current ?
Answer:
Given l1 = 39.5, l2 = 100 – 39.5 = 60.5 cm For a metre bridge, we have
To minimise resistance of the connections which are not accounted for in the bridge formula, we use thick copper strips.
On interchanging X and Y,
P : Q : : 1.53 : 1 or l1 : l2 : : 1.53 : 1
Thus the new balance point will be 60.5 cm from A.
(c) The galvanometer will show no current.
Question 11:
A storage battery of e.m.f. 8.0 V and internal resistance 0.5 is being charged by a 120 V d.c. supply using a series resistor of 15.5 . What is the terminal voltage of the battery during charging ? What is the purpose of having a series resistor in the charging circuit ?
Answer:
Total resistance of the circuit. = 15.5 + 0.5 = 16
Current through the cell drawn from the battery
E = V + Ir = 8 + 7.5 × 0.5 = 8 + 3.75 = 11.75 volt. The series resistor limits the current drawn from the external source. In its absence, the current will be dangerously high.
Question 12:
In a potentiometer arrangement, a cell of e.m.f. 1.25 V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm. What is the e.m.f. of the second cell ?
Answer:
Given
Question 13:
The number density of free electrons in a copper conductor estimated is 8.5 × 1028 m–3. How long does an electron take in drifting from one end of a wire 3.0 m long to its other end ? The area of cross-section of the wire is 2.0 × 10 –6 m2 and it is carrying a current of 3.0 A.
Answer:
n = 8.5 × 1028 m3; A = 2 × 10 –6 m2, I =
3.0A;
l = 3 m
I = dneA