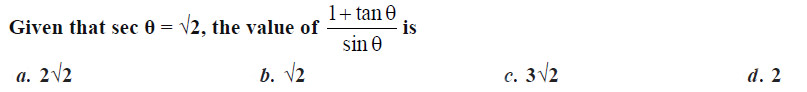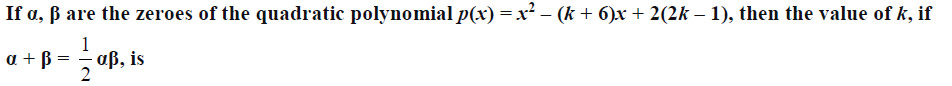Board Paper of Class 10 2022 Mathematics Standard Term-1 Set-4 Solutions - Solutions
General Instructions:
- This question paper contains 50 questions out of which 40 questions are to be attempted. All questions carry equal marks.
- This question paper contains three Sections: A, B, and C.
- Section A has 20 questions. Attempt any 16 questions from Q.No. 1 to 20.
- Section B has 20 questions. Attempt any 16 questions from Q.No. 21 to 40.
- Section C contains two Case Studies containing 5 Questions in each case. Attempt any 4 questions from Q.No. 41 to 45 and 4 another from Q.No. 46 to 50.
- There is only one correct option for every multiple choice question (MCQ). Marks will not be awarded for answering more than one option.
- There is no negative marking.
Question 1
The exponent of 5 in the prime factorisation of 3750 is
- 3
- 4
- 5
- 6
Ans: (b)
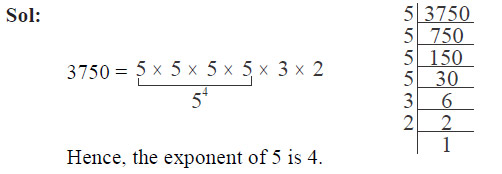
Question 2
The graph of a polynomial P(x) cuts the x-axis at 3 points and touches it at 2 other points. The number of zeroes of P(x) is
- 1
- 2
- 3
- 5
Ans: (d)
Sol: The number of zeroes of P(x) is 5.
Question 3
The values of x and y satisfying the two equations 32x + 33y = 34, 33x + 32y = 31 respectively are:
- –1, 2
- –1, 4
- 1, –2
- –1, –4
Ans: (a)

Question 4
If A(3, √3), B(0, 0) and C(3, k) are the three vertices of an equilateral triangle ABC, then the value of k is
- 2
- –3
- –√3
- –√2
Ans: (c)
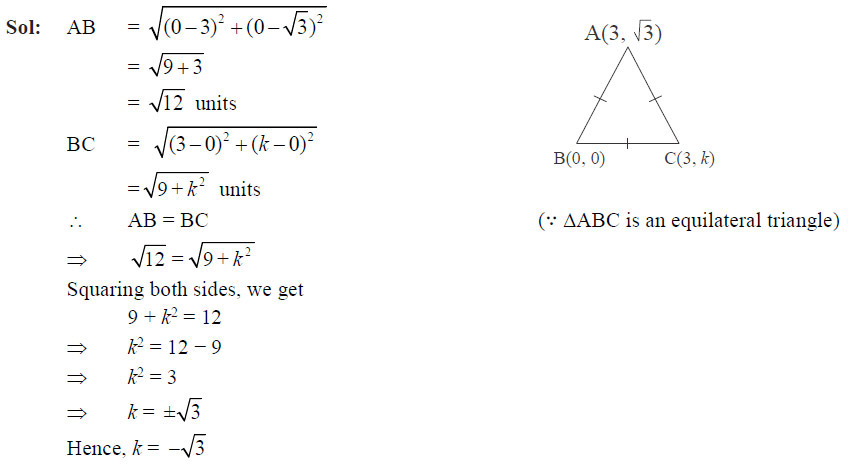
Question 5
In figure, DE || BC, AD = 2 cm and BD = 3 cm, then ar(ΔABC) : ar(ΔADE) is equal to
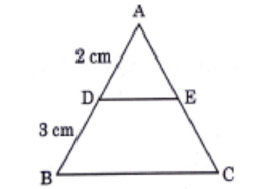
- 4 : 25
- 2 : 3
- 9 : 4
- 25 : 4
Ans: (d)

Question 6
If cot , the value of sec2 + cosec2 is
- 1
Ans: (d)

Question 7
The area of a quadrant of a circle where the circumference of circle is 176 m, is
- 2464 m2
- 1232 m2
- 616 m2
- 308 m2
Ans: (c)

Question 8
For an event E, P(E) + P() = x, then the value of x3 – 3 is
- –2
- 2
- 1
- –1
Ans. (a)
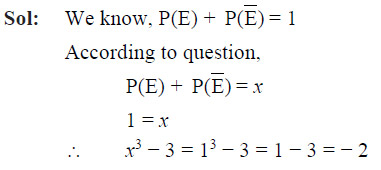
Question 9
What is the greatest possible speed at which a girl can walk 95 m and 171 m in an exact number of minutes?
- 17 m/min
- 19 m/min
- 23 m/min
- 13 m/min
Ans: (b)

Question 10
In figure, the graph of a polynomial P(x) is shown. The number of zeroes of P(x) is
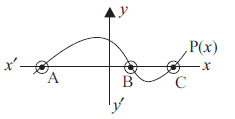
- 1
- 2
- 3
- 4
Ans: (c)
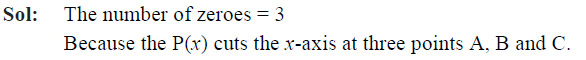
Question 11
Two lines are given to be parallel. The equation of one of the lines is 3x – 2y = 5. The equation of the second line can be
- 9x + 8y = 7
- –12x – 8y = 7
- –12x + 8y = 7
- 12x + 8y = 7
Ans: (c)

Question 12
Three vertices of a parallelogram ABCD are A(1, 4), B(–2, 3) and C(5, 8). The ordinate of the fourth vertex D is
- 8
- 9
- 7
- 6
Ans: (b)

Question 13
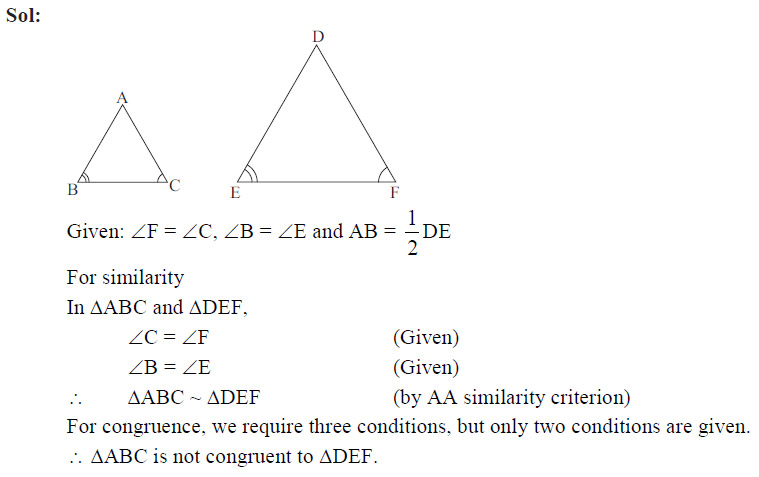
In ΔABC and ΔDEF, DE. Then, the two triangles are
- Congruent, but not similar.
- Similar, but not congruent.
- Neither congruent nor similar.
- Congruent as well as similar.
Ans: (b)
Question 14
In ΔABC right angled at B, sin A , then the value of cos C is
Ans: (a)

Question 15
The minute hand of a clock is 84 cm long. The distance covered by the tip of the minute hand from 10:10 am to 10:25 am is
- 44 cm
- 88 cm
- 132 cm
- 176 cm
Ans: (c)

Question 16
The probability that the drawn card from a pack of 52 cards is neither an ace nor a spade is
Ans: (a)

Question 17
Three alarm clocks ring their alarms at regular intervals of 20 min, 25 min and 30 min respectively. If they first beep together at 12 noon, at what time will they beep again for the first time?
- 4 : 00 pm
- 4 : 30 pm
- 5 : 00 pm
- 5 : 30 pm
Ans: (c)

Question 18
A quadratic polynomial, the product and sum of whose zeroes are 5 and 8 respectively is
- k [x2 – 8x + 5]
- k [x2 + 8x + 5]
- k [x2 – 5x + 8]
- k [x2 + 5x + 8]
Ans: (a)
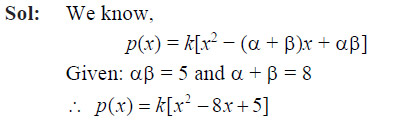
Question 19
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). The values of y are
- 1, –7
- –1, 7
- 2, 7
- –2, –7
Ans: (b)
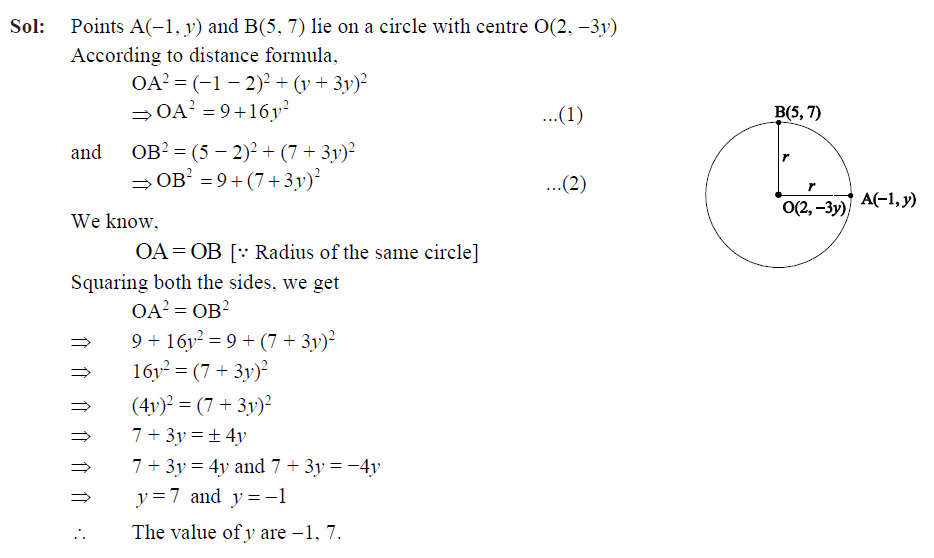
Question 20
Ans: (a)
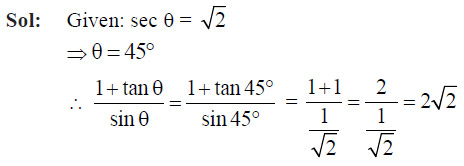
Question 21
The greatest number which when divides 1251, 9377 and 15628 leaves remainder 1, 2 and 3 respectively is
- 575
- 450
- 750
- 625
Ans: (d)

Question 22
Which of the following cannot be the probability of an event?
- 0.01
- 3%
Ans: (d)

Question 23
The diameter of a car wheel is 42 cm. The number of complete revolutions it will make in moving 132 km is
- 104
- 105
- 106
- 103
Ans: (b)

Question 24
If θ is an acute angle and tan θ + cot θ = 2, then the value of sin3 θ + cos3 θ is

Ans: (c)
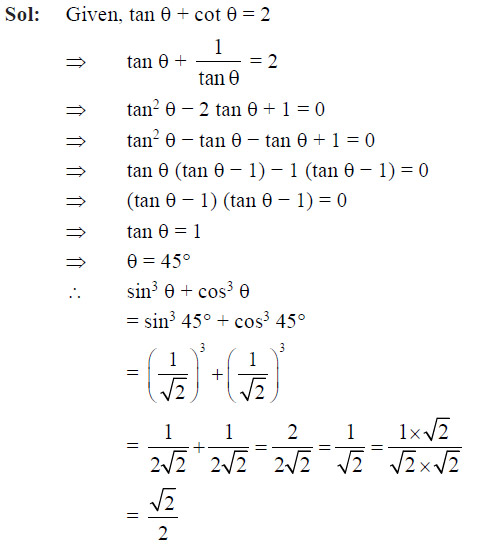
Question 25
The ratio in which the line 3x + y – 9 = 0 divides the line segment joining the points (1, 3) and (2, 7) is
- 3 : 2
- 2 : 3
- 3 : 4
- 4 : 3
Ans: (c)

Question 26
If x – 1 is a factor of the polynomial p(x) then
- a = 5, b = –1
- a = 9, b = –5
- a = 7, b = –3
- a = 3, b = 1
Ans: (b)

Question 27
If a and b are two coprime numbers, then a3 and b3 are
- Coprime
- Not coprime
- Even
- Odd
Ans: (a)
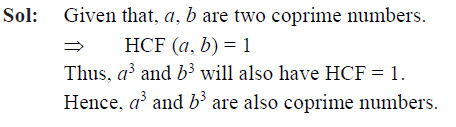
Question 28
The area of a square that can be inscribed in a circle of area cm2 is
- 321 cm2
- 642 cm2
- 128 cm2
- 256 cm2
Ans: (c)

Question 29
If A(4, –2), B(7, – 2) and C(7, 9) are the vertices of a ΔABC, then ΔABC is
- equilateral triangle
- isosceles triangle
- right angled triangle
- isosceles right angled triangle
Ans: (c)

Question 30
- –7
- 7
- -3
- 3
Ans: (b)
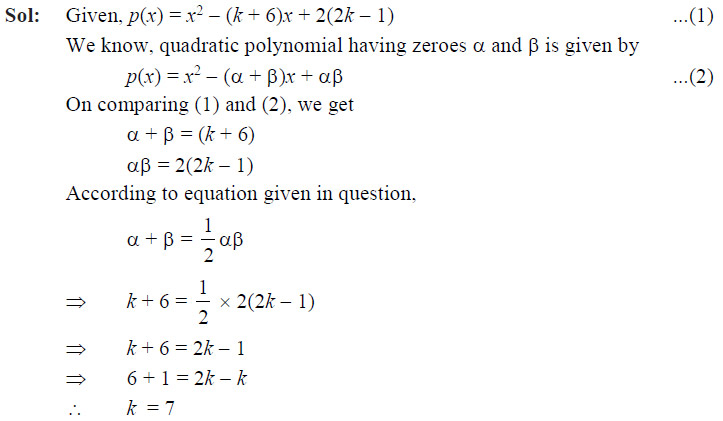
Question 31
If n is a natural number, then 2(5n + 6n) always ends with
- 1
- 4
- 3
- 2
Ans: (d)
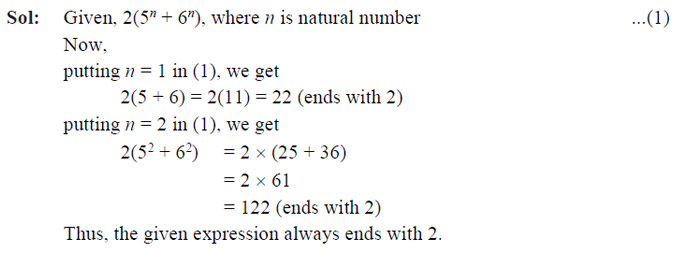
Question 32
The line segment joining the points P(–3, 2) and Q(5, 7) is divided by the y-axis in the ratio
- 3 : 1
- 3 : 4
- 3 : 2
- 3 : 5
Ans: (d)
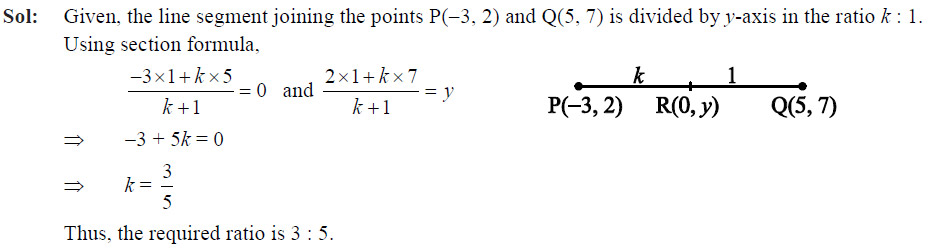
Question 33
If a cot θ + b cosec θ = p and b cot θ + a cosec θ = q, then p2 – q2 =
- a2 – b2
- b2 – a2
- a2 + b2
- b – a
Ans: (b)
Question 34
If the perimeter of a circle is half to that of a square, then the ratio of the area of the circle to the area of the square is
- 22 : 7
- 11 : 7
- 7 : 11
- 7 : 22
Ans: (d)
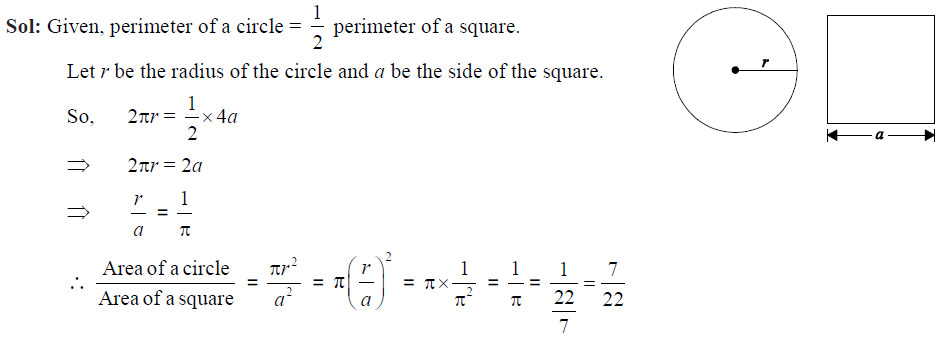
Question 35
A dice is rolled twice. The probability that 5 will not come up either time is
Ans: (d)
Sol: A dice is rolled twice. Then possible outcomes are :
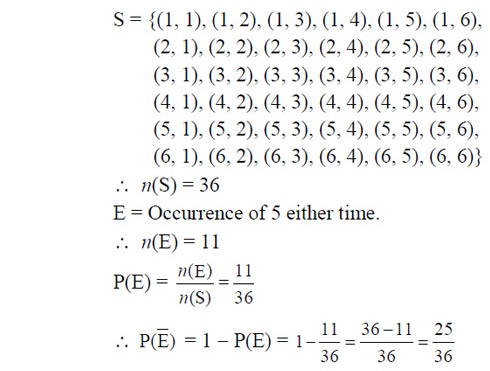
Question 36
The LCM of two numbers is 2400. Which of the following CANNOT be their HCF?
- 300
- 400
- 500
- 600
Ans: (c)

Question 37
In fig., PA, QB and RC are each perpendicular to AC. If x = 8 cm and z = 6 cm, then y is equal to
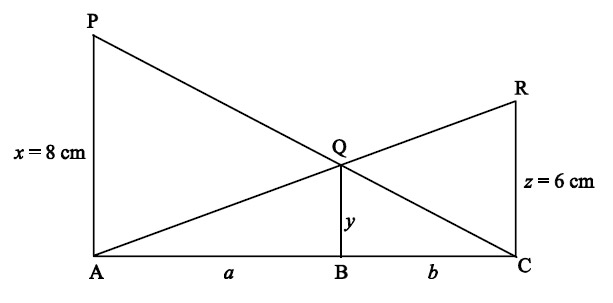
- cm
- cm
- cm
- cm
Ans: (d)

Question 38
In a
- 107°
- 135°
- 155°
- 145°
- 107°
- 135°
- 155°
- 145°
Ans: (a)

Question 39
If sec θ + tan θ = p, then tan θ is
Ans: (b)
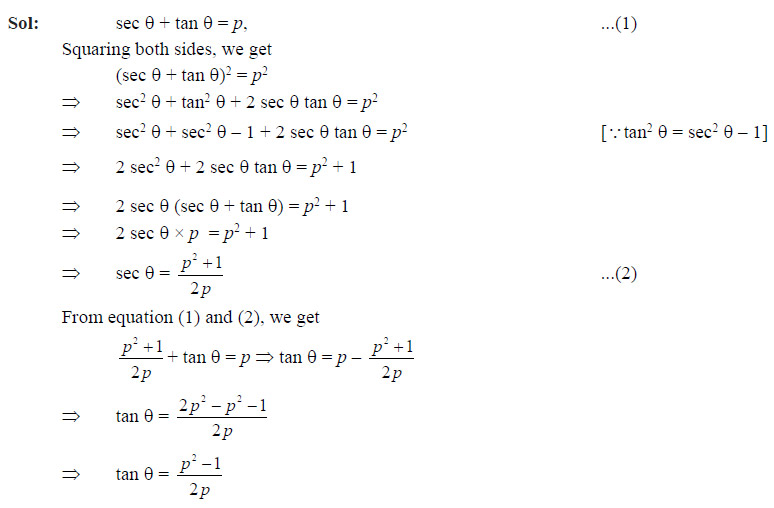
Question 40
The base BC of an equilateral ΔABC lies on the y-axis. The coordinates of C are (0, –3). If the origin is the mid-point of the base BC, what are the coordinates of A and B?

Ans: (c)


Based on the above information, answer any four of the following questions :
Given information:
Let, fixed charge for 2 days = ₹x.
and additional charge (per day) = ₹y.
Question 41
The situation of amount paid by Radhika, is algebraically represented by
- x – 4y = 16
- x + 4y = 16
- x – 2y = 16
- x + 2y = 16
Ans: (d)
The amount paid by Radhika, for keeping the book for 4 days = ₹16
Fixed charge for two days + additional charge (per day) for next 2 days = ₹16
x + 2y = 16
Question 42
The situation of amount paid by Amruta, is algebraically represented by
- x – 2y = 11
- x – 2y = 11
- x + 4y = 22
- x – 4y = 11
Ans: (c)
Sol: The amount paid by Amruta, for keeping the book for 6 days = ₹22
Fixed charge for two days + additional charge (per day) for next 4 days = ₹22.
x + 4y = 22
Question 43
What are the fixed charges for a book?
- ₹9
- ₹10
- ₹13
- ₹15
Ans: (b)
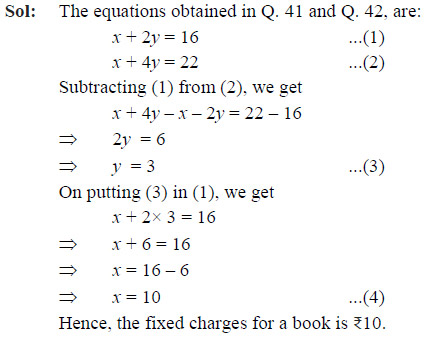
Question 44
What are the additional charges for each subsequent day for a book?
- ₹6
- ₹5
- ₹4
- ₹3
Ans: (d)
Sol: The additional charges for each subsequent day for a book = y = ₹3 (As solved in Q. 43 equation (3).)
Question 45
What is the total amount paid by both, if both of them have kept the book for 2 more days?
- ₹35
- ₹52
- ₹50
- ₹58
Ans: (c)
Sol: Total amount = Amount paid by Radhika for keeping the book for 6 days + Amruta for keeping the book for 8 days
= Radhika for keeping the book for 4 days + 2 days additional
+ Amruta keeping the book for 6 days + 2 days additional
= 16 + 2y + 22 + 2y
= 38 + 4y
= 38 + 4 × 3
= 38 + 12
= ₹50
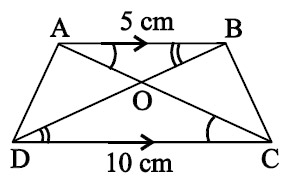
Question 46
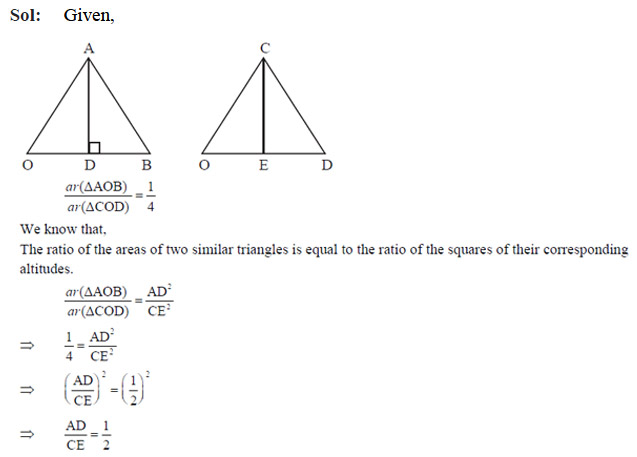
The two triangular regions AOB and COD are
- Similar by AA criterion
- Similar by AA criterion
- Similar by RHS criterion
- Not similar
Ans: (a)
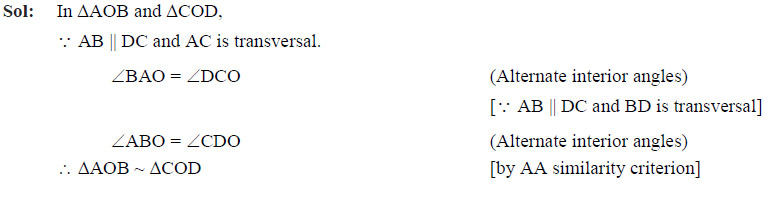
Question 47
The ratio of the area of the ΔAOB to the area of ΔCOD, is
- 4 : 1
- 1 : 4
- 1 : 2
- 2 : 1
Ans: (b)
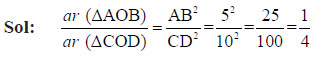
Question 48
If the ratio of the perimeter of ΔAOB to the perimeter of ΔCOD would have been 1 : 4, then
- AB = 2 CD
- AB = 4 CD
- CD = 2 AB
- CD = 4 AB
Ans: (d)
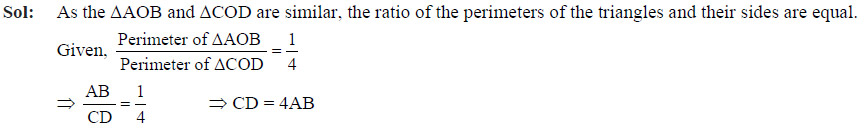
Question 49
If in Δs AOD and BOC, , then
Ans: (b)

Question 50
If the ratio of areas of two similar triangles AOB and COD is 1 : 4, then which of the following statements is true?
- The ratio of their perimeters is 3 : 4.
- The corresponding altitudes have a ratio 1 : 2.
- The medians have a ratio 1 : 4.
- The angle bisectors have a ratio 1 : 16.
Ans: (b)