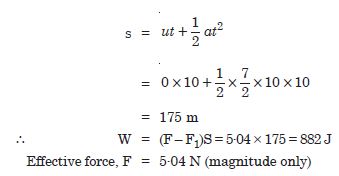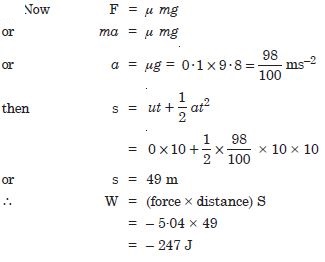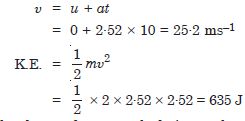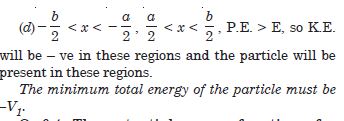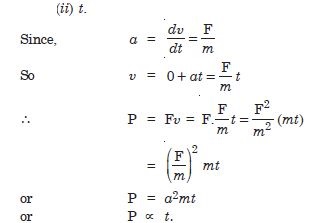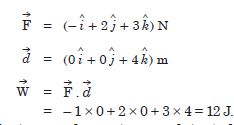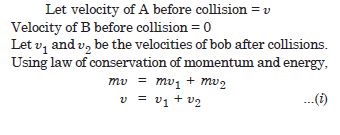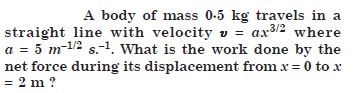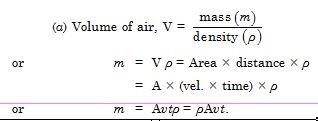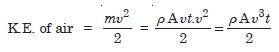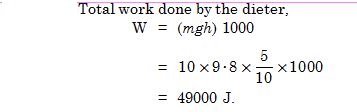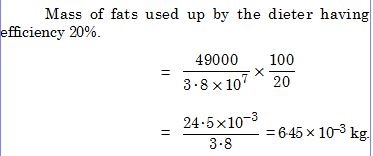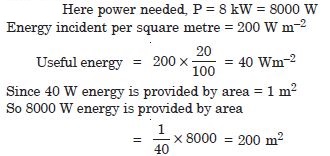NCERT Solutions for Class 11 Physics Chapter 6 - Work, Energy and Power

Question 1:

The sign of work done by a force on body is important to understand. State carefully if the following quantity is + ve or – ve.
Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.

Question 2:

The sign of work done by a force on body is important to understand. State carefully if the following quantity is + ve or – ve.
Work done by gravitational force in the above case.

Question 3:

The sign of work done by a force on body is important to understand. State carefully if the following quantity is + ve or – ve.
Work done by friction on a body sliding down an inclined plane.

Question 4:

The sign of work done by a force on body is important to understand. State carefully if the following quantity is + ve or – ve.
Work done by applied force on a body moving on a rough horizontal plane with uniform velocity.

Question 5:

The sign of work done by a force on body is important to understand. State carefully if the following quantity is + ve or – ve.
Work done by resistive force of air on a vibrating pendulum in bringing it to rest.

Question 6:

A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with co-efficient of kinetic friction = 0.1. Compute the work done by the applied force in 10 s

Question 7:

A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with co-efficient of kinetic friction = 0.1. Compute the work done by friction in 10 s

Question 8:

A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with co-efficient of kinetic friction = 0.1. Compute the work done by the net force on the body in 10 s

Question 9:

A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with co-efficient of kinetic friction = 0.1. Compute the change in kinetic energy of the body in 10 s, and interpret your results.

Question 10:

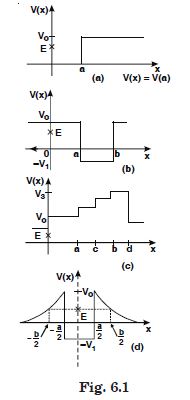
Given below are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contents for which these potential energy shapes are relevant.

Question 11:

Question 12:

Answer the following :
The casting of a rocket in flight burns up due to friction. At whose expense the heat energy required for burning is obtained—the rocket or the atmosphere ?

Question 13:

Answer the following :
Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why ?

Question 14:

Answer the following :
An artificial satellite orbiting the earth in very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth ?

Question 15:

Answer the following :
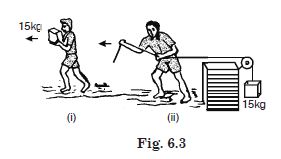
In figure (i), the man walks 2 m carrying a mass of 15 kg on his hands. In figure (ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley and a mass of 15 kg hangs at its other end. In which case is the work done larger ?

Question 16:

Underline the correct alternative :
When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered.

Question 17:

Underline the correct alternative :
Work done by a body against friction always results in a loss of its kinetic/potential energy.

Question :18

Underline the correct alternative :
The rate of change of total momentum of a many particle system is proportional to the external force/sum of the internal forces of the system.

Question 19:

Underline the correct alternative :
In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total energy of the system of two bodies.

Question 20:

State if each of the following statements is true or false. Give reasons for your answer.
In an elastic collision of two bodies, the momentum and energy of each body is conserved.

Question 21:

State if each of the following statements is true or false. Give reasons for your answer.
Total energy of a system is always conserved, no matter what internal and external forces on the body are present.

Question 22:

State if each of the following statements is true or false. Give reasons for your answer.
Work done in the motion of a body over a closed loop is zero for every force in nature.

Question 23:

State if each of the following statements is true or false. Give reasons for your answer.
In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.

Question 24:

Answer carefully, with reasons :
In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls i.e., when they are in contact ?

Question 25:

Answer carefully, with reasons :
Is the total linear momentum conserved during the short time of an elastic collision of two balls ?

Question 26:

Answer carefully, with reasons :
What are the answers to (a) and (b) for an inelastic collision ?

Question 27:

Answer carefully, with reasons :
If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic ? (Note. we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).

Question 28:

A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
(i) t^1/2 (ii) t (iii) t^3/2 (iv) t².

Question 29:

A body is moving uni-directionally under the influence of a source of constant power. Its displacement in time t is proportional to : (i) t^1/2 (ii) t (iii) t^3/2 (iv) t².

Question 30:

Question 31:

Question 32:

A rain drop of radius 2 mm falls from a height of 500 m above the ground. It falls with decreasing acceleration due to viscous resistance of the air until at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is work done by the gravitational force on the drop in the first half and second half of its journey ? What is the work done by resistive force in the entire journey if its speed on reaching the ground is 10 m s^–1 ?

Question 33:

A molecule in a gas container hits the wall with speed 200 ms^–1 and angle 30° with the normal and rebounds with the same speed. Is momentum conserved in the collision ? Is the collision elastic or inelastic ?

Question 34:

A pump on the ground floor of a building can pump up water to fill a tank of volume 30 m3 in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump ?

Question 35:

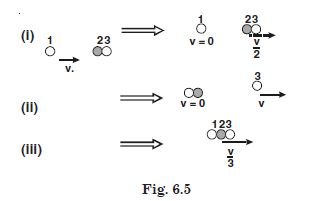
Two identical ball-bearings in contact with each other and resting on a frictionless table are hit head-on collision by another ball bearing of same mass moving initially with a speed u. If the collision is elastic, which of the following is a possible result after collision.

Question 36:

The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table as shown. How does the bob A rise after the collision ? Neglect the size of the bobs and assume the collision to be elastic.

Question 37:

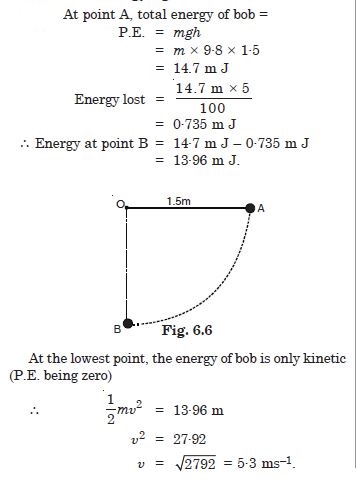
The bob of a pendulum is released from a horizontal position A as shown in Fig. 6.6. If the length of the pendulum is 1·5 m, what is the speed with which the bob arrives at the lowermost point B, given that it dissipates 5% of its initial energy against air resistance ?

Question 38:

A trolley of mass 300 kg carrying a sand bag of 25 kg is moving uniformly with a speed of 27 km h–1 on a frictionless track. After a while, sand starts leaking out of a hole on the trolley’s floor at rate of 0·05 kg s^–1. What is the speed of the trolley after the entire sand bag is empty ?

Question 39:

Question 40:

The blades of a windmill sweep out a circle of area A.
If the wind flows at a velocity $\mathrm{\upsilon }$ perpendicular to the circle, what is the mass of the air passing through it in time t ?

Question 41:

The blades of a windmill sweep out a circle of area A.
What is the kinetic energy of the air ?

Question 42:

The blades of a windmill sweep out a circle of area A.
Assume that the windmill converts 25% of the wind energy into electrical energy and that A = 30 m², u = 36 km/h and the density of air is 1.2 kg m^–3. What is the electrical power produced ?

Question 42:

A person trying to lose weight (dieter) lifts a 10 kg mass 0·5 m, 1000 times. Assume that the potential energy lost each time she lowers the mass is dissipated.
How much work does she do against the gravitational force ?

Question 43:

A person trying to lose weight (dieter) lifts a 10 kg mass 0·5 m, 1000 times. Assume that the potential energy lost each time she lowers the mass is dissipated.
Fat supplies 3·8 × 10⁷ J of energy per kilogram which is converted to mechanical energy with a 20% efficiency rate. How much fat will the dieter use up ?

Question 44:

A family uses 8 kW of power
Direct solar energy is incident on the horizontal surface at an average rate of 200 W per square metre. If 20% of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW ?

Question 45:

A family uses 8 kW of power Compare this area to that of the roof of a typical house.

Question 46:

Give the location of the centre of mass of a sphere