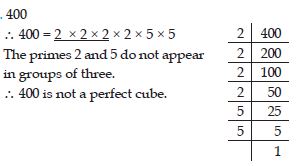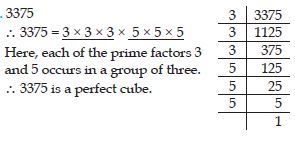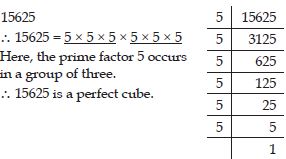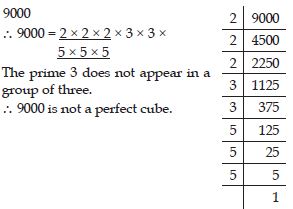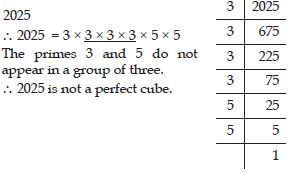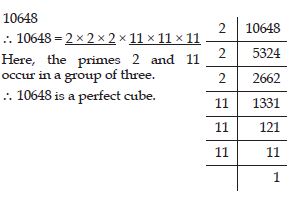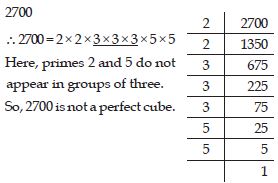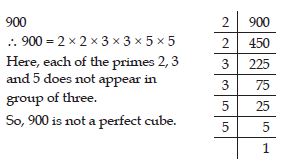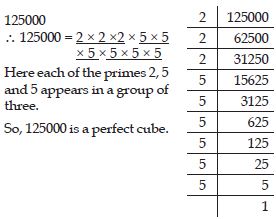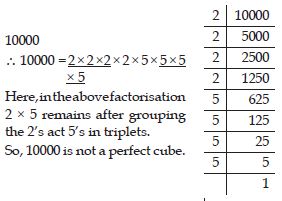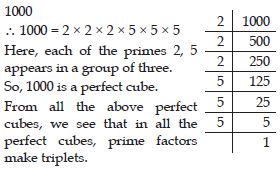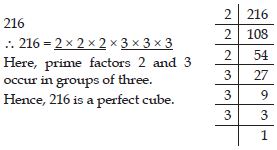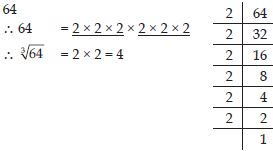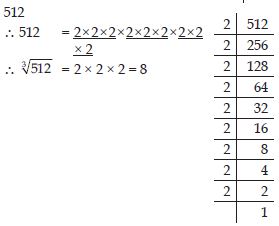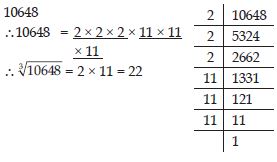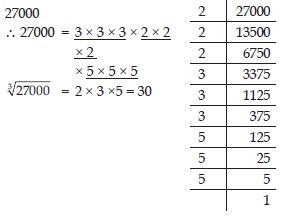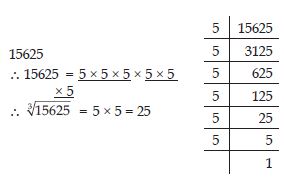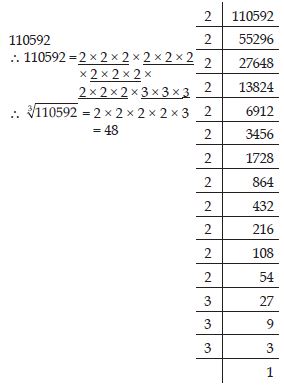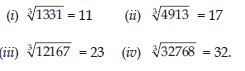NCERT Solutions for Class 8 Cubes and Cube Roots | Aasoka

Question 1:

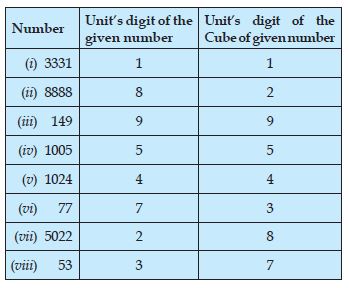
Find the one’s digit of the cube of each of the following numbers.
(i) 3331 (ii) 8888 (iii) 149
(iv) 1005 (v) 1024 (vi) 77
(vii) 5022 (viii) 53

Answer:

As we know that, the cube of a number ending in 0, 1, 4, 5, 6 and 9 ends in 0, 1, 4, 5, 6 and 9 respectively. However, the cube of a number ending in 2 ends in 8 and vice-versa. Similarly, the cube of a number ending in 3 or 7 ends in 7 or 3 respectively. Thus, by looking at the unit digit of a given number, we can determine the unit’s digit of its cube. Now, unit’s digit of the cube of each of the asked numbers is as follows:

Show Answer

Question 2:

Express the following number as the sum of odd numbers using the above pattern.
6³

Answer:

6³ = 216 = 31 + 33 + 35 + 37 + 39 + 41

Show Answer

Question 3:

Express the following number as the sum of odd numbers using the above pattern.
8³

Answer:

8³ = 512 = 57 + 59 + 61 + 63 + 65 + 67 + 69 + 71

Show Answer

Question 4:

Express the following number as the sum of odd numbers using the above pattern.
7³

Answer:

7³ = 343 = 43 + 45 + 47 + 49 + 51 + 53 + 55

Show Answer

Question 5:

Consider the following pattern:
2³ - 1³ = 1 + 2 x 1 x 3
3³ - 2³ = 1 + 3 x 2 x 3
4³ - 3³ = 1 + 4 x 3 x 3
Using the above pattern, find the value of the following:
7³ - 6³

Answer:

7³ – 6³
According to the given pattern:
7³ – 6³ = 1 + 7 x 6 x 3

Show Answer

Question 6:

Consider the following pattern: 2³ – 1³ = 1 + 2 x 1 x 3
3³ – 2³ = 1 + 3 x 2 x 3
4³ – 3³ = 1 + 4 x 3 x 3
Using the above pattern, find the value of the
following:
12³ – 11³

Answer:

12³ – 11³
According to the given pattern:
12³ – 11³ = 1 + 12 x 11 x 3

Show Answer

Question 7:

Consider the following pattern: 2³ – 1³ = 1 + 2 x 1 x 3
3³ – 2³ = 1 + 3 x 2 x 3
4³ – 3³ = 1 + 4 x 3 x 3
Using the above pattern, find the value of the following:
20³ – 19³

Answer:

20³ – 19³
According to the given pattern:
20³ – 19³ = 1 + 20 x 19 x 3

Show Answer

Question 8:

Consider the following pattern:
2³ – 1³ = 1 + 2 x 1 x 3
3³ – 2³ = 1 + 3 x 2 x 3
4³ – 3³ = 1 + 4 x 3 x 3
Using the above pattern, find the value of the following:
51³ – 50³

Answer:

51³ – 50³
According to the given pattern:
51³ – 50³ = 1 + 51 x 50 x 3

Show Answer

Question 9:

Check whether 400 is perfect cube or not.

Answer:

Show Answer

Question 10:

Check whether 3375 is perfect cube or not.

Answer:

Show Answer

Question 11:

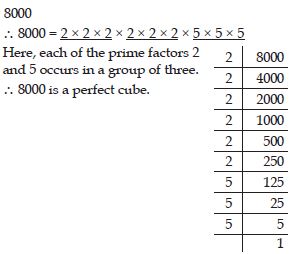
Check whether 8000 is perfect cube or not.

Answer:

Show Answer

Question 12:

Check whether 15625 is perfect cube or not.

Answer:

Show Answer

Question 13:

Check whether 9000 is perfect cube or not.

Answer:

Show Answer

Question 14:

Check whether 6859 is perfect cube or not.

Answer:

Show Answer

Question 15:

Check whether 2025 is perfect cube or not.

Answer:

Show Answer

Question 16:

Check whether 10648 is perfect cube or not.

Answer:

Show Answer

Question 17:

Check whether 2700 is perfect cube or not.

Answer:

Show Answer

Question 18:

Check whether 16000 is perfect cube or not.

Answer:

Show Answer

Question 19:

Check whether 64000 is perfect cube or not.

Answer:

Show Answer

Question 20:

Check whether 900 is perfect cube or not.

Answer:

Show Answer

Question 21:

Check whether 125000 is perfect cube or not.

Answer:

Show Answer

Question 22:

Check whether 36000 is perfect cube or not.

Answer:

Show Answer

Question 23:

Check whether 21600 is perfect cube or not.

Answer:

Show Answer

Question 24:

Check whether 10000 is perfect cube or not.

Answer:

Show Answer

Question 25:

Check whether 27000000 is perfect cube or not.

Answer:

Show Answer

Question 26:

Check whether 1000 is perfect cube or not.

Answer:

Show Answer

Question 27:

Check whether 216 is perfect cube or not.

Answer:

Show Answer

Question 28:

Check whether 128 is perfect cube or not.

Answer:

Show Answer

Question 29:

Check whether 1000 is perfect cube or not.

Answer:

Show Answer

Question 30:

Check whether 100 is perfect cube or not.

Answer:

Show Answer

Question 31:

Check whether 46656 is perfect cube or not.

Answer:

Show Answer

Question 32:

Find the smallest number by which 243 must be multiplied to obtain a perfect cube.

Answer:

243 = 3 × 3 × 3 × 3 × 3
We note that, prime factor 3 appears in a group of 3. Further, we are left with two more factors 3.
So, if we multiply 3 × 3 by 3 i.e., then in the product 3 will appear in one more group of three and the product will be a perfect cube. i.e.,
243 × 3 = 3 × 3 × 3 × 3 × 3 × 3 = 729
which is a perfect cube.
Hence, the smallest whole number by which 243 should be multiplied to make a perfect cube is 3.

Show Answer

Question 33:

Find the smallest number by which 256 must be multiplied to obtain a perfect cube.

Answer:

256
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
We note that, prime factor appears in groups of 3. Further, we are left with two more factors 2.
To make it a perfect cube, we need one more 2.
In that case:
256 × 2 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 512
which is a perfect cube.
Hence, the smallest whole number by which 256 should be multiplied to make it a perfect cube is 2.

Show Answer

Question 34:

Find the smallest number by which 72 must be multiplied to obtain a perfect cube.

Answer:

72
72 = 2 × 2 × 2 × 3 × 3
We note that, prime factor 2 appears in groups of 3. Further, we are left with two more factors 3.
To make it a perfect cube, we need one more 3.
In that case:
72 × 3 = 2 × 2 × 2 × 3 × 3 × 3 = 216
which is a perfect cube.
Hence, the smallest whole number by which 72 should be multiplied to make it a perfect cube is 3.

Show Answer

Question 35:

Find the smallest number by which 675 must be multiplied to obtain a perfect cube.

Answer:

675
$∴$ 675 = 3 × 3 × 3 × 5 × 5
We note that, in prime factorisation of 675, prime factor 3 appears in a group of 3. Further, we are left with two more factors 5.
To make it a perfect cube, we need one more 5.
In that case:
675 × 5 = 3 × 3 × 3 × 5 × 5 × 5 = 3375
which is a perfect cube.
Hence, the smallest whole number by which 675 should be multiplied to make it a perfect cube is 5.

Show Answer

Question 36:

Find the smallest number by which 100 must be multiplied to obtain a perfect cube.

Answer:

100
100 = 2 × 2 × 5 × 5
We note that, in the prime factorisation of 100, the prime factors 2 and 5 are not in groups of 3.
$∴$ We have, one more 2 and one more 5 to make them in groups of 3.
In that case:
100 × 2 × 5 = 2 × 2 × 2 × 5 × 5 × 5 = 1000
which is a perfect cube.
Hence, the smallest whole number by which 100 should be multiplied to make it a perfect cube is 10.

Show Answer

Question 37:

Find the smallest number by which 81 must be divided to obtain a perfect cube.

Answer:

81
$∴$ 81 = 3 × 3 × 3 × 3
The prime factor 3 does not appear in a group of three.
$∴$ 81 is not a perfect cube.
In the prime factorisation of 81, one factor 3 remains ungrouped.
So, 81 is not a perfect cube.
If we divide 81 by 3, then the prime factorisation of the quotient becomes 81 ÷ 3 = 3 × 3 × 3 = 27 which is a perfect cube.
Hence, the smallest number by which 81 should be divided to make it a perfect cube is 3.

Show Answer

Question 38:

Find the smallest number by which 128 must be divided to obtain a perfect cube.

Answer:

128
$∴$ 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
In the prime factorisation of 128, one factor 2 remains ungrouped.
So, 128 is not a perfect cube.
If we divide 128 by 2, then the prime factorisation of the quotient becomes 128 ÷ 2 = 2 × 2 × 2 × 2 × 2 × 2 = 64
which is a perfect cube.
Hence, the smallest number by which 128
should be divided to make it perfect cube is 2.

Show Answer

Question 39:

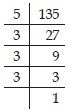
Find the smallest number by which 135 must be divided to obtain a perfect cube.

Answer:

135
$∴$ 135 = 3 × 3 × 3 × 5
In the prime factorisation of 135, the factor 5 remains ungrouped.
So, 135 is not a perfect cube.
If we divide 135 by 5, then the prime factorisation of the quotient becomes 135 ÷ 5 = 3 × 3 × 3 = 27
which is a perfect cube.
Hence, the smallest number by which 135 should be divided to make it a perfect cube is 5.

Show Answer

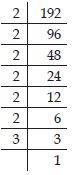
Question 40:

Find the smallest number by which 192 must be divided to obtain a perfect cube.192
$∴$ 192 = 2 × 2 × 2 × 2 × 2 × 2 × 3
In the prime factorisation of 192, the factor 3 remains ungrouped.
So, 192 is not a perfect cube.
If we divide 192 by 3, then the prime factorisation of the quotient becomes
192 ÷ 3 = 2 × 2 × 2 × 2× 2× 2 = 64
which is a perfect cube.
Hence, the smallest number by which 192
should be divided to make it a perfect cube is 3.

Answer:

192
$∴$ 192 = 2 × 2 × 2 × 2 × 2 × 2 × 3
In the prime factorisation of 192, the factor 3 remains ungrouped.
So, 192 is not a perfect cube.
If we divide 192 by 3, then the prime factorisation of the quotient becomes
192 ÷ 3 = 2 × 2 × 2 × 2× 2× 2 = 64
which is a perfect cube.
Hence, the smallest number by which 192
should be divided to make it a perfect cube is 3.

Show Answer

Question 41:

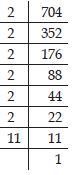
Find the smallest number by which 704 must be divided to obtain a perfect cube.

Answer:

704
$∴$ 704 = 2 × 2 × 2 × 2 × 2 × 2 × 11
In the prime factorisation of 704, the factor 11 remains ungrouped.
So, 704 is not a perfect cube.
If we divide 704 by 11, then the prime factorisation of the quotient becomes 704 ÷ 11 = 2 × 2 × 2 × 2 × 2 × 2
= 64
which is a perfect cube.
Hence, the smallest number by which 704 should be divided to make it a perfect cube is 11.

Show Answer

Question 42:

Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?

Answer:

The sides of cuboid are 5 cm, 2 cm and 5 cm.
Volume of the plastic in = 2 × 5 × 5 cm³
Here, the prime factors of 2 and 5 are not in groups of three.
$∴$ We have to multiply by 2 × 2 × 5 i.e., by 20 to make it a perfect cube.

Show Answer

Question 43:

Find the cube root of 64 by prime factorisation method.

Answer:

Show Answer

Question 44:

Find the cube root of 512 by prime factorisation method.

Answer:

Show Answer

Question 45:

Find the cube root of 10648 by prime factorisation method.

Answer:

Show Answer

Question 46:

Find the cube root of 27000 by prime factorisation method.

Answer:

Show Answer

Question 47:

Find the cube root of 15625 by prime factorisation method.

Answer:

Show Answer

Question 48:

Find the cube root of 13824 by prime factorisation method.

Answer:

Show Answer

Question 49:

Find the cube root of 110592 by prime factorisation method.

Answer:

Show Answer

Question 50:

Find the cube root of 46656 by prime factorisation method.

Answer:

Show Answer

Question 51:

Find the cube root of 175616 by prime factorisation method.

Answer:

Show Answer

Question 52:

Find the cube root of 91125 by prime factorisation method.

Answer:

Show Answer

Question 53:

Cube of any odd number is even.

TRUE
FALSE

Answer:

FALSE

Show Answer

Question 54:

A perfect cube does not end with two zeros.

TRUE
FALSE

Answer:

TRUE

Show Answer

Question 55:

If square of a number ends with 5, then its cube ends with 25.

TRUE
FALSE

Answer:

TRUE

Show Answer

Question 56:

There is no perfect cube which ends with 8

TRUE
FALSE

Answer:

FALSE

Show Answer

Question 57:

The cube of two digit number may be a three digit number.

TRUE
FALSE

Answer:

FALSE

Show Answer

Question 58:

The cube of a two digit number may have seven or more digits.

TRUE
FALSE

Answer:

FALSE

Show Answer

Question 59:

The cube of a single digit number may be a single digit number.

TRUE
FALSE

Answer:

TRUE

Show Answer

Question 60:

You are told that 1331 is a perfect cube. Can you guess without factorisation what is its cube root? Similarly, guess the cube roots of 4913, 12167, 32768.

Answer:

Show Answer